• 算法
• 参数
• 例子
  • 问题

遗传算法的本质是一种并行，高效，全局搜索的方法

遗传算法将问题的解根据实际情况进行编码并将其视为单独的个体，使用编码的交换，突变来产生下一代种群，每次迭代使用适当的评估函数评价个体（解）的适应度，循环迭代取得相对最优的解。

算法

来自wikipedia

选择初始种群
循环

评价适应程度
产生下一种群（适应度越高，选择概率越大）

直到达到停止条件

停止条件可能包括：

• 找到了最优值
• 适应度已饱和？？
• 进化次数限制
• 时间限制
• 人为干预

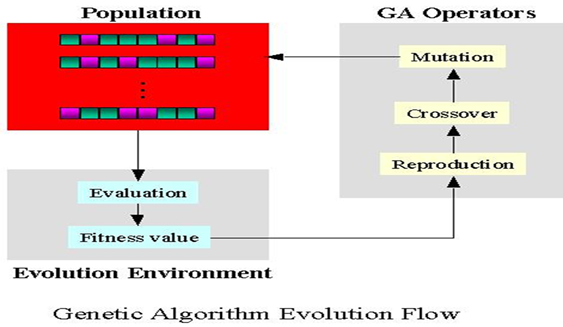
一般在产生下一种群的过程中，还包括个体编码的交换和随机变异，如下图中的描述。图片来自boat_lee。

参数

• 种群规模（P,population size）
• 编码长度（I,string length）
• 交叉概率（pc，probability of performing crossover）
• 变异概率（pm，probability of mutation）
• 终止条件（termination criteria）

例子

GA算法可以用来求解优化问题，下面用GA算法来解一个简单的0-1背包问题

问题描述：

有 N 件物品和一个容量为 V 的背包。第 i 件物品的费用是 c[i]，价值是 w[i]。求解将哪些物品装入背包可使价值总和最大。

import numpy as np

#设置参数
episodes = 10
capacity  = 200
goods = np.array([[20,30],[40,75],[80,100],[60,90],[6,8],[50,50]])

population_size = 25
pc = 0.6
pm = 0.2
code_len = goods.shape[0]

#记录
history = {}
#相关函数定义
def compute_weight_value(p,goods):
    """
    计算所选物品的重量和价值
    """
    w_v = np.dot(p,goods)
    w = w_v[:,0]
    v = w_v[:,1]
    out_of_capacity = np.argwhere(w>capacity)
    v[out_of_capacity]=0
    return w,v

def select(p,v,n):
    """
    轮盘赌方式选取子代
    """
    prob = v/v.sum()
    prob_ = prob.cumsum()
    selected = np.zeros(shape=(n,code_len),dtype=np.uint32)
    for i in range(n):
        idx = np.argwhere(np.random.rand()<prob_)[0]
        selected[i,:] = p[idx,:]
    return selected

def mutation(p):
    """
    变异函数
    pm=0.2
    """
    for i in range(p.shape[0]):
        if np.random.rand()<pm:
            p[i,:] = np.bitwise_xor(p[i,:], np.random.randint(2,size=(1,p.shape[1])))
    return p

def crossover(p):
    """
    编码交叉
    """
    cross_len = int(code_len/2)
    selected = np.zeros(shape=(2,p.shape[1]),dtype=np.uint32)
    idx=[0,0]
    selected_num = 0
    for i in range(p.shape[1]):
        if np.random.rand()<pc:
            selected[selected_num] = p[i,:]
            idx[selected_num] = i
            selected_num +=1
            if selected_num//2>0:
                p[idx[0],:] = np.concatenate((selected[0,:cross_len],selected[1,cross_len:]))
                p[idx[1],:] = np.concatenate((selected[1,:cross_len],selected[0,cross_len:]))
                selected_num%=2
    return p

#随机产生初始种群
population = np.random.randint(2,size=(population_size,code_len),dtype=np.uint32)

#主循环
for i in range(episodes):
    w,v = compute_weight_value(population,goods)
    p_ = select(population,v,population_size)
    p_ = crossover(p_)
    p_ = mutation(p_)
    population = p_
    history[i] = [w[np.argmax(v)],v.max()]
history

{0: [186, 273],
 1: [186, 273],
 2: [186, 273],
 3: [186, 273],
 4: [186, 273],
 5: [200, 295],
 6: [200, 295],
 7: [200, 295],
 8: [200, 295],
 9: [200, 295]}

问题

由于遗传算法得到的是近似的最优解，在多次运行时并不能每次都得到最优解（不太适合背包问题）

实现方面的要点为适应函数和编码（二进制编码，浮点编码，符号编码）

更详细的文章